[algorithms] Bloom Filter 布隆過濾器

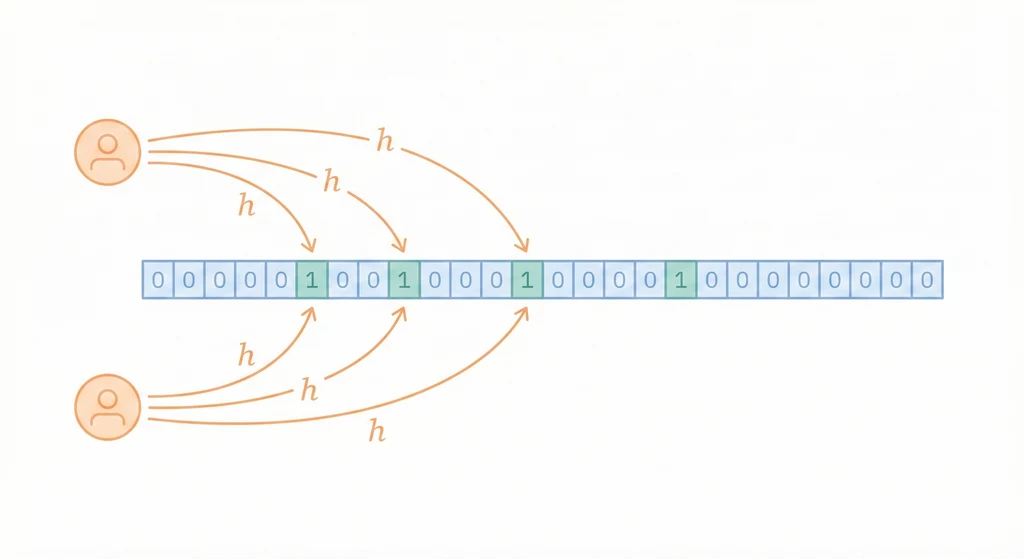
視覺化概覽

graph TD
    E["'apple'"] --> H1["hash1"]
    E --> H2["hash2"]
    E --> H3["hash3"]

    H1 --> |"idx=2"| B2
    H2 --> |"idx=5"| B5
    H3 --> |"idx=8"| B8

    subgraph 位元陣列["Bit Array"]
        B0["0"] --- B1["0"] --- B2["1"] --- B3["0"] --- B4["0"] --- B5["1"] --- B6["0"] --- B7["0"] --- B8["1"] --- B9["0"]
    end

    style B2 fill:#c8e6c9,stroke:#4caf50
    style B5 fill:#c8e6c9,stroke:#4caf50
    style B8 fill:#c8e6c9,stroke:#4caf50
    style E fill:#e3f2fd,stroke:#1976d2

什麼是布隆過濾器？

布隆過濾器是一種空間效率極高的概率型資料結構，用於判斷元素是否存在於集合中。

回答「一定不存在」或「可能存在」
               ↓
         ┌──────────┐
  x →    │  Bloom   │ → false: 一定不在集合中
         │  Filter  │ → true:  可能在集合中（有誤判率）
         └──────────┘

原理

位元陣列（初始全 0）:
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

添加 "apple"（3 個雜湊函數）:
hash1("apple") = 2
hash2("apple") = 5
hash3("apple") = 8
[0, 0, 1, 0, 0, 1, 0, 0, 1, 0]

添加 "banana":
hash1("banana") = 1
hash2("banana") = 5   ← 衝突！
hash3("banana") = 7
[0, 1, 1, 0, 0, 1, 0, 1, 1, 0]

查詢 "cherry":
hash1("cherry") = 2  → bits[2] = 1 ✓
hash2("cherry") = 4  → bits[4] = 0 ✗ → 一定不存在！

查詢 "grape":
hash1("grape") = 1  → bits[1] = 1 ✓
hash2("grape") = 5  → bits[5] = 1 ✓
hash3("grape") = 8  → bits[8] = 1 ✓
→ 可能存在（但其實是誤判！）

關鍵特性

特性	說明
空間效率	遠小於存儲實際元素
假陽性	可能說「存在」但實際不在
無假陰性	說「不存在」一定不在
不可刪除	刪除會影響其他元素
不可列舉	無法取出已添加的元素

最佳參數

給定 n（預期元素數）和 p（誤判率）：

位元陣列大小 m = -n × ln(p) / (ln2)²
雜湊函數數量 k = (m/n) × ln2

元素數	誤判率	位元數	雜湊函數
1,000	1%	9,585	7
10,000	1%	95,851	7
100,000	0.1%	1,437,759	10

實作要點

雙重雜湊技巧

// 用 2 個雜湊函數模擬 k 個
int hash_i(String item, int i) {
    return (hash1(item) + i * hash2(item)) % m;
}

應用場景

1. 快取穿透防護 - 擋掉不存在的 key
2. 垃圾郵件過濾 - 快速過濾已知垃圾
3. URL 去重 - 爬蟲避免重複抓取
4. 資料庫查詢優化 - 避免不必要的磁碟 I/O
5. 分散式系統 - 節點間快速同步狀態

變體

變體	特點
Counting Bloom Filter	支持刪除（計數器替代位元）
Cuckoo Filter	支持刪除，空間更小
Quotient Filter	支持合併和調整大小

相關檔案

• Java 實作：BloomFilter.java