[algorithms] Skip List 跳躍表

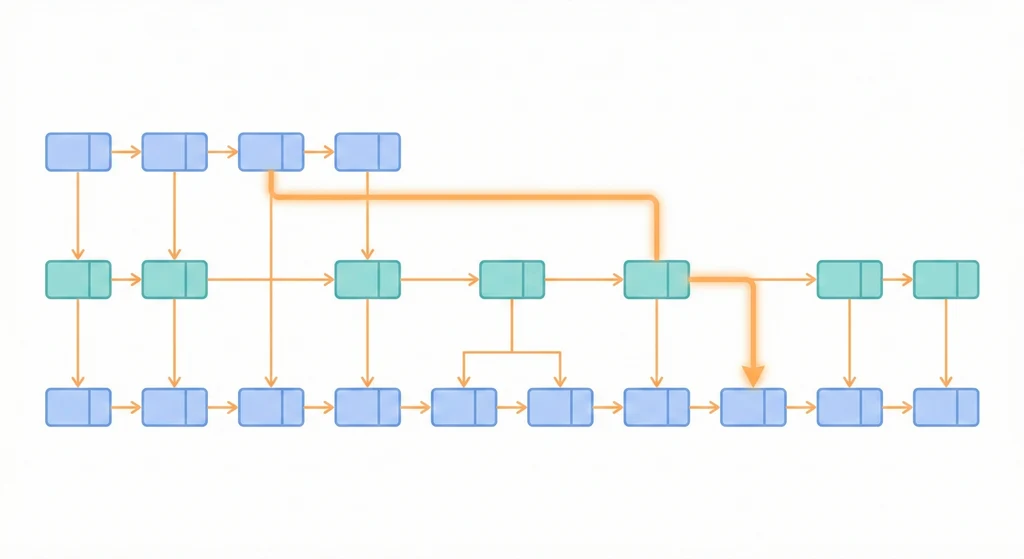
視覺化概覽

graph LR
    subgraph L3["Level 3（快速通道）"]
        H3["HEAD"] --> N25_3["25"] --> NULL3["null"]
    end
    subgraph L2["Level 2"]
        H2["HEAD"] --> N7_2["7"] --> N25_2["25"] --> NULL2["null"]
    end
    subgraph L1["Level 1"]
        H1["HEAD"] --> N3_1["3"] --> N7_1["7"] --> N12_1["12"] --> N25_1["25"] --> NULL1["null"]
    end
    subgraph L0["Level 0（完整資料）"]
        H0["HEAD"] --> N3_0["3"] --> N6_0["6"] --> N7_0["7"] --> N9_0["9"] --> N12_0["12"] --> N19_0["19"] --> N25_0["25"] --> NULL0["null"]
    end

    H3 -.-> H2 -.-> H1 -.-> H0
    N25_3 -.-> N25_2 -.-> N25_1 -.-> N25_0
    N7_2 -.-> N7_1 -.-> N7_0
    N12_1 -.-> N12_0
    N3_1 -.-> N3_0

    style L3 fill:#e8f5e9,stroke:#4caf50
    style L0 fill:#fff3e0,stroke:#ff9800

什麼是跳躍表？

跳躍表是一種基於多層有序鏈表的資料結構，通過隨機化實現期望 O(log n) 的查找。

Level 3:  HEAD ──────────────────────── 25 ──── null
Level 2:  HEAD ────── 7 ────────────── 25 ──── null
Level 1:  HEAD ── 3 ── 7 ──── 12 ──── 25 ──── null
Level 0:  HEAD ── 3 ── 6 ── 7 ── 9 ── 12 ── 19 ── 25 ── null

核心思想

就像書的目錄：

• Level 0 = 完整內容（每一頁）
• Level 1 = 章節目錄
• Level 2 = 大章目錄
• Level 3 = 全書總覽

查找時從最高層開始，逐層向下細化。

操作

查找

查找 19:
Level 3: HEAD → 25 (25 > 19, 下降)
Level 2: HEAD → 7 → 25 (25 > 19, 下降)
Level 1: HEAD → 3 → 7 → 12 → 25 (25 > 19, 下降)
Level 0: ... → 12 → 19 ✓ 找到！

插入

1. 找到插入位置（同時記錄每層的前驅）
2. 隨機決定新節點的層數
3. 在對應層中插入

int randomLevel() {
    int level = 0;
    while (level < MAX_LEVEL && random.nextDouble() < 0.5) {
        level++;
    }
    return level;
}

刪除

1. 找到目標節點
2. 在每一層中移除
3. 更新最高層數

複雜度

操作	平均	最差
查找	O(log n)	O(n)
插入	O(log n)	O(n)
刪除	O(log n)	O(n)
空間	O(n)	O(n log n)

跳躍表 vs 平衡樹

	Skip List	AVL / Red-Black Tree
實作難度	簡單	複雜
區間查詢	天然支持	需要中序遍歷
並發支持	容易（局部鎖）	困難
平衡方式	隨機化	旋轉操作
記憶體	指標較多	固定

應用

1. Redis 有序集合（Sorted Set） - zset 底層
2. LevelDB / RocksDB - MemTable
3. 並發資料結構 - ConcurrentSkipListMap (Java)

經典題目

1. 設計跳表 - LeetCode 1206

相關檔案

• Java 實作：SkipList.java