[algorithms] Deque 雙端佇列

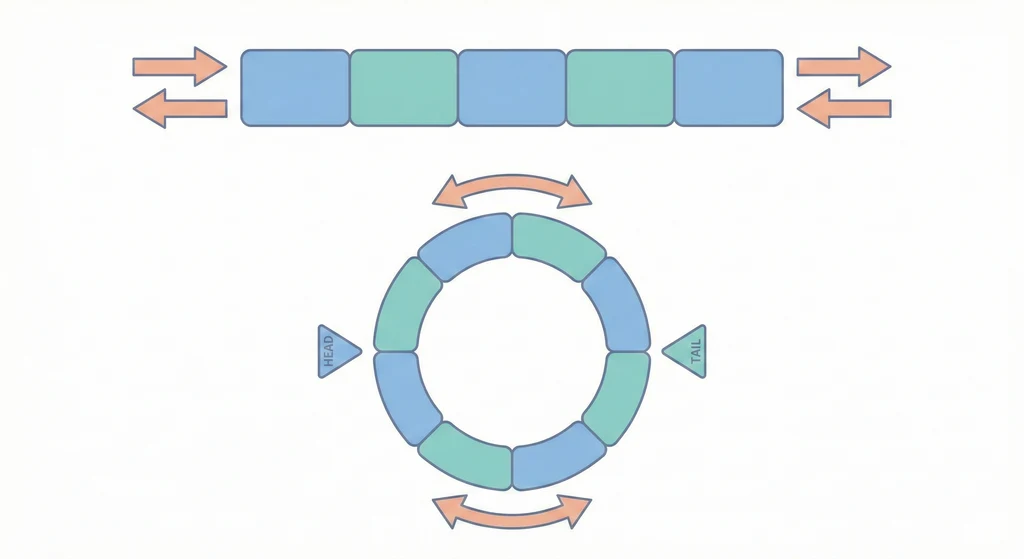
視覺化概覽

graph LR
    AF["addFirst()"] --> |插入| Front
    RF["removeFirst()"] --> |移除| Front

    subgraph Deque["雙端佇列"]
        Front["前端"] --- A["A"] --- B["B"] --- C["C"] --- D["D"] --- Rear["後端"]
    end

    AL["addLast()"] --> |插入| Rear
    RL["removeLast()"] --> |移除| Rear

    style Front fill:#bbdefb,stroke:#1976d2
    style Rear fill:#c8e6c9,stroke:#4caf50
    style Deque fill:#fafafa,stroke:#9e9e9e

什麼是雙端佇列？

Deque（Double-Ended Queue）是一種兩端都可以插入和刪除的線性資料結構。

        addFirst →  ┌───┬───┬───┬───┐  ← addLast
    removeFirst ←   │ A │ B │ C │ D │  → removeLast
                    └───┴───┴───┴───┘
                   front              rear

與 Stack / Queue 的關係

操作	Stack	Queue	Deque
前端插入	-	-	addFirst
前端刪除	-	dequeue	removeFirst
後端插入	push	enqueue	addLast
後端刪除	pop	-	removeLast

Deque 可以同時當 Stack 和 Queue 使用。

實作方式

雙向鏈表

null ← [A] ⇄ [B] ⇄ [C] ⇄ [D] → null
        ↑                    ↑
       head                 tail

所有操作 O(1)。

環形陣列

[ _ | A | B | C | D | _ | _ | _ ]
      ↑               ↑
     head             tail

addFirst → head = (head - 1 + capacity) % capacity
addLast  → tail = (tail + 1) % capacity

操作複雜度

操作	時間複雜度
addFirst / addLast	O(1)
removeFirst / removeLast	O(1)
peekFirst / peekLast	O(1)
size / isEmpty	O(1)

常見應用

1. 滑動視窗最大值 - 單調雙端佇列
2. 工作竊取算法 - 多執行緒排程
3. 瀏覽器歷史 - 前進/後退
4. 撤銷/重做 - 編輯器

滑動視窗最大值

// 使用單調遞減 Deque
Deque<Integer> deque = new ArrayDeque<>();
for (int i = 0; i < n; i++) {
    // 移除超出視窗的
    while (!deque.isEmpty() && deque.peekFirst() < i - k + 1)
        deque.pollFirst();
    // 保持單調遞減
    while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i])
        deque.pollLast();
    deque.offerLast(i);
    // 記錄結果
    if (i >= k - 1) result[i-k+1] = nums[deque.peekFirst()];
}

經典題目

1. 滑動視窗最大值 - LeetCode 239
2. 設計循環雙端佇列 - LeetCode 641

相關檔案

• Java 實作：Deque.java