[algorithms] Fenwick Tree (BIT) 樹狀陣列

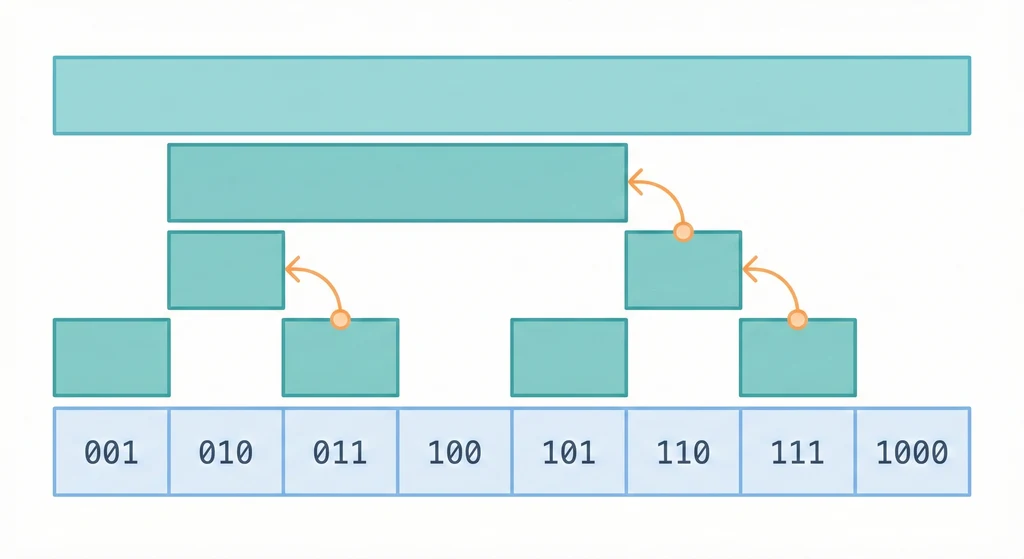
視覺化概覽

graph TD
    T8["tree[8] 管理 [1,8]"] --> T4["tree[4] 管理 [1,4]"]
    T8 --> T6["tree[6] 管理 [5,6]"]
    T4 --> T2["tree[2] 管理 [1,2]"]
    T4 --> T3["tree[3] 管理 [3,3]"]
    T6 --> T5["tree[5] 管理 [5,5]"]
    T6 --> T7["tree[7] 管理 [7,7]"]
    T2 --> T1["tree[1] 管理 [1,1]"]

    style T3 fill:#e3f2fd,stroke:#1976d2
    style T4 fill:#bbdefb,stroke:#1976d2
    style T8 fill:#90caf9,stroke:#1976d2

    linkStyle 0 stroke:#f44336,stroke-width:2
    linkStyle 2 stroke:#f44336,stroke-width:2
    linkStyle 6 stroke:#f44336,stroke-width:2

紅色路徑：更新 arr[1] 時需沿 1→2→4→8 向上更新父節點

什麼是 Fenwick Tree？

比線段樹更簡潔的區間查詢結構。

又稱 Binary Indexed Tree (BIT)，利用二進位的巧妙性質。

陣列:  [1, 3, 5, 7, 9, 11, 13, 15]
索引:   1  2  3  4  5  6   7   8

BIT:
tree[1] = arr[1]         = 1          管理 [1,1]
tree[2] = arr[1..2]      = 1+3 = 4    管理 [1,2]
tree[3] = arr[3]         = 5          管理 [3,3]
tree[4] = arr[1..4]      = 16         管理 [1,4]
tree[5] = arr[5]         = 9          管理 [5,5]
tree[6] = arr[5..6]      = 20         管理 [5,6]
tree[7] = arr[7]         = 13         管理 [7,7]
tree[8] = arr[1..8]      = 64         管理 [1,8]

lowbit 核心

lowbit(x) = x 的最低位 1 代表的數值

x = 6  → 二進位 110  → lowbit = 2 (10)
x = 12 → 二進位 1100 → lowbit = 4 (100)
x = 8  → 二進位 1000 → lowbit = 8 (1000)

公式：lowbit(x) = x & (-x)

lowbit 與管理範圍

索引 i	二進位	lowbit	管理範圍
1	001	1	[1, 1]
2	010	2	[1, 2]
3	011	1	[3, 3]
4	100	4	[1, 4]
5	101	1	[5, 5]
6	110	2	[5, 6]
7	111	1	[7, 7]
8	1000	8	[1, 8]

規律：tree[i] 管理 arr[i - lowbit(i) + 1 ... i]

核心操作

1. 前綴和查詢 - O(log n)

查詢 prefixSum(7):

7 (111)  → 加 tree[7]，減 lowbit → 6
6 (110)  → 加 tree[6]，減 lowbit → 4
4 (100)  → 加 tree[4]，減 lowbit → 0
結束

結果 = tree[7] + tree[6] + tree[4]

int prefixSum(int i) {
    int sum = 0;
    while (i > 0) {
        sum += tree[i];
        i -= lowbit(i);
    }
    return sum;
}

2. 單點更新 - O(log n)

更新 arr[3] += delta:

3 (011)  → 更新 tree[3]，加 lowbit → 4
4 (100)  → 更新 tree[4]，加 lowbit → 8
8 (1000) → 更新 tree[8]，加 lowbit → 16 > n
結束

void update(int i, int delta) {
    while (i <= n) {
        tree[i] += delta;
        i += lowbit(i);
    }
}

3. 區間和查詢

int rangeSum(int left, int right) {
    return prefixSum(right) - prefixSum(left - 1);
}

視覺化

索引:  1   2   3   4   5   6   7   8
      ┌───┬───┬───┬───┬───┬───┬───┬───┐
arr:  │ 1 │ 3 │ 5 │ 7 │ 9 │11 │13 │15 │
      └───┴───┴───┴───┴───┴───┴───┴───┘
           ↓       ↓       ↓       ↓
tree[1]=1 ─┘   tree[3]=5 ─┘   tree[5]=9 ─┘   tree[7]=13─┘
              ↓               ↓               ↓
tree[2]=4 ────┘   tree[4]=16 ─┘   tree[6]=20 ─┘
                              ↓
tree[8]=64 ───────────────────┘

Fenwick Tree vs Segment Tree

特性	Fenwick Tree	Segment Tree
程式碼	~15 行	~50 行
空間	O(n)	O(4n)
常數	更小	較大
前綴和	✓ 原生支援	需要查 [0, i]
區間最值	✗ 不支援	✓ 支援
區間更新	技巧性較高	Lazy Prop

選擇建議：

• 只需要前綴和/區間和 → Fenwick Tree
• 需要區間最值或複雜查詢 → Segment Tree

2D Fenwick Tree

支援 2D 矩陣的區間和查詢：

void update(int x, int y, int delta) {
    for (int i = x; i <= n; i += lowbit(i))
        for (int j = y; j <= m; j += lowbit(j))
            tree[i][j] += delta;
}
 
int prefixSum(int x, int y) {
    int sum = 0;
    for (int i = x; i > 0; i -= lowbit(i))
        for (int j = y; j > 0; j -= lowbit(j))
            sum += tree[i][j];
    return sum;
}

時間複雜度

操作	時間
建樹	O(n log n)
單點更新	O(log n)
前綴和查詢	O(log n)
區間和查詢	O(log n)

經典應用

1. 動態前綴和
2. 逆序對計數
3. 區間和查詢
4. 2D 矩陣區域和

經典題目

1. 區間和查詢 - LeetCode 307
2. 計算右側較小元素 - LeetCode 315
3. 2D 區域和 - LeetCode 308
4. 逆序對 - 劍指 Offer 51

相關檔案

• Java 實作：FenwickTree.java