[algorithms] Segment Tree 線段樹

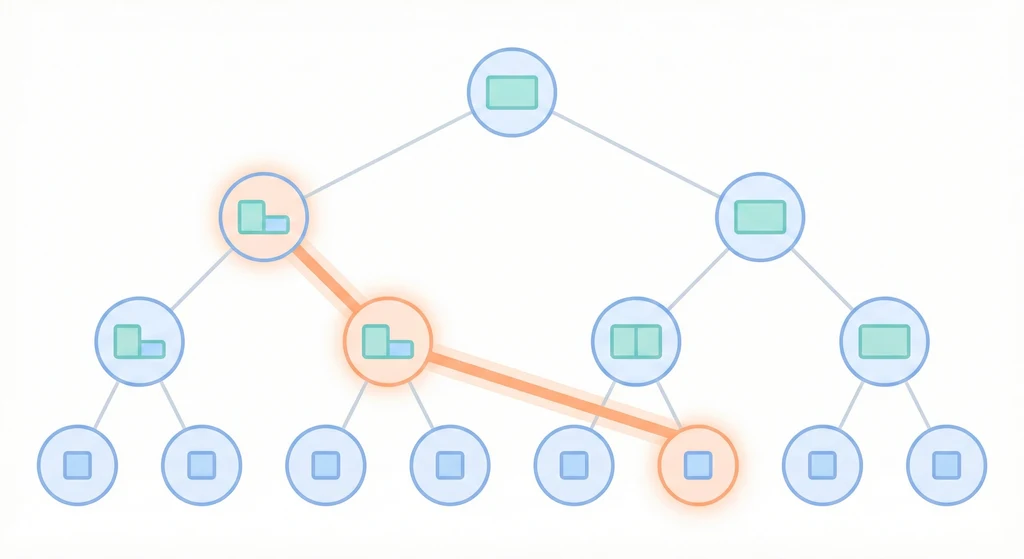
視覺化概覽

graph TD
    R["[0,5] sum=36"] --> L["[0,2] sum=9"]
    R --> Ri["[3,5] sum=27"]
    L --> LL["[0,1] sum=4"]
    L --> LR["[2] =5"]
    Ri --> RL["[3,4] sum=16"]
    Ri --> RR["[5] =11"]
    LL --> LLL["[0] =1"]
    LL --> LLR["[1] =3"]
    RL --> RLL["[3] =7"]
    RL --> RLR["[4] =9"]

    style LLR fill:#ffcc80,stroke:#ff9800
    style LR fill:#ffcc80,stroke:#ff9800
    style RL fill:#ffcc80,stroke:#ff9800

    linkStyle 4 stroke:#ff9800,stroke-width:2
    linkStyle 2 stroke:#ff9800,stroke-width:2
    linkStyle 3 stroke:#ff9800,stroke-width:2

橘色節點為查詢 [1,4] 時命中的區間：[1] + [2] + [3,4] = 24

什麼是線段樹？

專門處理區間問題的樹狀結構。

陣列: [1, 3, 5, 7, 9, 11]

          [0,5]=36
         /        \
    [0,2]=9      [3,5]=27
    /    \        /    \
 [0,1]=4 [2]=5 [3,4]=16 [5]=11
  /  \          /   \
[0]=1 [1]=3  [3]=7 [4]=9

每個節點存儲該區間的和

解決什麼問題？

頻繁的區間查詢 + 更新

問題：給定陣列，多次詢問區間和，並可能修改元素

暴力法：
- 查詢 [L, R] 的和：O(n)
- q 次查詢：O(qn)

線段樹：
- 查詢 [L, R] 的和：O(log n)
- q 次查詢：O(q log n)

核心操作

1. 建樹 Build - O(n)

void build(int node, int start, int end) {
    if (start == end) {
        tree[node] = arr[start];  // 葉節點
    } else {
        int mid = (start + end) / 2;
        build(左子節點, start, mid);
        build(右子節點, mid+1, end);
        tree[node] = tree[左] + tree[右];  // 合併
    }
}

2. 區間查詢 Query - O(log n)

查詢 [1, 4] 的和：

          [0,5]
         /     \
    [0,2]      [3,5]
    /   \       /   \
 [0,1] [2]   [3,4] [5]
  /  \        /  \
[0] [1]    [3] [4]

需要的節點：[1] + [2] + [3,4]
           = 3 + 5 + 16 = 24

int query(int node, int start, int end, int L, int R) {
    // 完全不重疊
    if (R < start || L > end) return 0;
 
    // 完全包含
    if (L <= start && end <= R) return tree[node];
 
    // 部分重疊，拆分
    int mid = (start + end) / 2;
    return query(左, start, mid, L, R) +
           query(右, mid+1, end, L, R);
}

3. 單點更新 Update - O(log n)

更新 arr[2] = 10（原本是 5）

          [0,5] +5
         /        \
    [0,2] +5     [3,5]
    /    \
 [0,1]  [2] +5

只更新包含該點的節點

支援的查詢類型

類型	合併方式	預設值
區間和	a + b	0
區間最小值	min(a, b)	+∞
區間最大值	max(a, b)	-∞
區間 GCD	gcd(a, b)	0
區間乘積	a × b	1

進階：Lazy Propagation

問題：區間更新太慢

把 [0, 1000000] 都加 5
一個一個更新：O(n log n) 太慢！

解法：懶標記

// 區間 [L, R] 每個元素都加 val
void updateRange(int node, int start, int end, int L, int R, int val) {
    // 有懶標記要先下推
    if (lazy[node] != 0) pushDown(node);
 
    if (R < start || L > end) return;
 
    if (L <= start && end <= R) {
        // 完全包含，打懶標記
        tree[node] += (end - start + 1) * val;
        lazy[node] += val;
        return;
    }
 
    // 部分重疊
    int mid = (start + end) / 2;
    updateRange(左, start, mid, L, R, val);
    updateRange(右, mid+1, end, L, R, val);
    tree[node] = tree[左] + tree[右];
}

時間複雜度

操作	無 Lazy	有 Lazy
建樹	O(n)	O(n)
單點更新	O(log n)	O(log n)
區間更新	O(n log n)	O(log n)
區間查詢	O(log n)	O(log n)

空間複雜度

O(4n) ≈ O(n)

線段樹 vs 其他方案

方案	單點更新	區間查詢	區間更新
暴力	O(1)	O(n)	O(n)
前綴和	O(n)	O(1)	O(n)
線段樹	O(log n)	O(log n)	O(log n)
Fenwick Tree	O(log n)	O(log n)	O(log n)

經典應用

1. 區間和查詢
2. 區間最值查詢（RMQ）
3. 計數問題
4. 動態維護排序

經典題目

1. 區間和查詢 - LeetCode 307
2. 區間最大值 - 常見面試題
3. 逆序對計數 - LeetCode 315
4. 天際線問題 - LeetCode 218

相關檔案

• Java 實作：SegmentTree.java