[algorithms] AVL Tree 自平衡二元搜尋樹

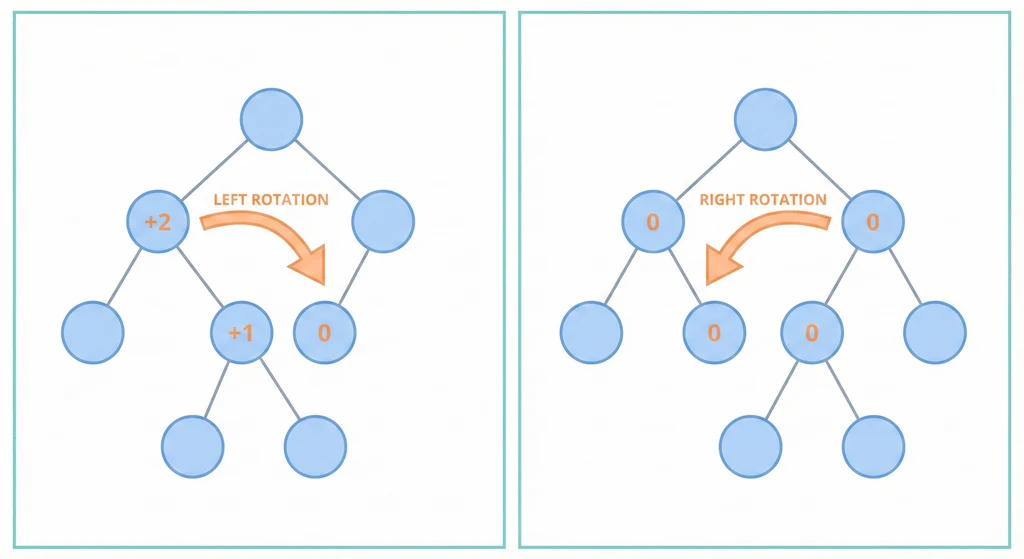
視覺化概覽

graph LR
    subgraph 旋轉前["RR 不平衡"]
        A1["z (BF=-2)"] --> B1[" "]
        A1 --> C1["y (BF=-1)"]
        C1 --> D1[" "]
        C1 --> E1["x"]
        style B1 fill:none,stroke:none
        style D1 fill:none,stroke:none
    end

    旋轉前 -- "左旋轉" --> 旋轉後

    subgraph 旋轉後["平衡後"]
        A2["y (BF=0)"] --> B2["z"]
        A2 --> C2["x"]
    end

    style 旋轉前 fill:#fff3e0,stroke:#ff9800
    style 旋轉後 fill:#e8f5e9,stroke:#4caf50

什麼是 AVL Tree？

BST + 自動平衡 = 保證 O(log n)

普通 BST 插入 1,2,3,4,5:     AVL Tree 插入 1,2,3,4,5:

1                                  2
 \                                / \
  2                              1   4
   \                                / \
    3          vs                  3   5
     \
      4
       \
        5

高度 = 5（退化成鏈表）         高度 = 3（保持平衡）

平衡因子（Balance Factor）

BF = 左子樹高度 - 右子樹高度

AVL 規則：|BF| ≤ 1

     30 (BF=1)
    /  \
   20   40 (BF=0)
  /
 10

BF(30) = 2 - 1 = 1 ✓
BF(40) = 0 - 0 = 0 ✓

四種不平衡情況

1. Left-Left (LL) → 右旋轉

      z                 y
     /                 / \
    y       →         x   z
   /
  x

插入在左子樹的左邊

2. Right-Right (RR) → 左旋轉

  z                     y
   \                   / \
    y       →         z   x
     \
      x

插入在右子樹的右邊

3. Left-Right (LR) → 左旋轉 + 右旋轉

    z              z              x
   /              /              / \
  y      →       x      →       y   z
   \            /
    x          y

插入在左子樹的右邊

4. Right-Left (RL) → 右旋轉 + 左旋轉

  z            z                x
   \            \              / \
    y    →       x     →      z   y
   /              \
  x                y

插入在右子樹的左邊

旋轉操作詳解

右旋轉

Node rightRotate(Node y) {
    Node x = y.left;
    Node B = x.right;
 
    x.right = y;
    y.left = B;
 
    updateHeight(y);
    updateHeight(x);
 
    return x;
}

左旋轉

Node leftRotate(Node x) {
    Node y = x.right;
    Node B = y.left;
 
    y.left = x;
    x.right = B;
 
    updateHeight(x);
    updateHeight(y);
 
    return y;
}

插入步驟

1. 標準 BST 插入
2. 回溯更新高度
3. 檢查平衡因子
4. 如果不平衡，執行旋轉

Node insert(Node node, int value) {
    // 1. BST 插入
    if (node == null) return new Node(value);
 
    if (value < node.value)
        node.left = insert(node.left, value);
    else
        node.right = insert(node.right, value);
 
    // 2. 更新高度
    updateHeight(node);
 
    // 3. 檢查並旋轉
    int balance = getBalance(node);
 
    // LL
    if (balance > 1 && value < node.left.value)
        return rightRotate(node);
 
    // RR
    if (balance < -1 && value > node.right.value)
        return leftRotate(node);
 
    // LR
    if (balance > 1 && value > node.left.value) {
        node.left = leftRotate(node.left);
        return rightRotate(node);
    }
 
    // RL
    if (balance < -1 && value < node.right.value) {
        node.right = rightRotate(node.right);
        return leftRotate(node);
    }
 
    return node;
}

刪除步驟

1. 標準 BST 刪除
2. 回溯更新高度
3. 重新平衡（可能需要多次旋轉）

時間複雜度

操作	時間複雜度
搜尋	O(log n)
插入	O(log n)
刪除	O(log n)
旋轉	O(1)

AVL vs 其他樹

樹	平衡條件	搜尋	插入/刪除
BST	無	O(n) 最差	O(n) 最差
AVL	嚴格（BF≤1）	O(log n)	O(log n)
Red-Black	寬鬆	O(log n)	O(log n)

AVL vs Red-Black Tree

• AVL：更平衡，搜尋更快，但插入/刪除旋轉較多
• Red-Black：稍不平衡，但插入/刪除更快

選擇：

• 讀多寫少 → AVL
• 讀寫均衡 → Red-Black（Java TreeMap/TreeSet）

實際應用

1. 資料庫索引：需要快速搜尋
2. 記憶體管理：快速查找空閒區塊
3. 編譯器符號表：快速變數查找

視覺化範例

插入順序: 10, 20, 30

Step 1: 插入 10
    10

Step 2: 插入 20
    10
      \
       20

Step 3: 插入 30 → RR 不平衡 → 左旋轉
    10              20
      \            /  \
       20    →    10   30
        \
         30

相關檔案

• Java 實作：AVLTree.java