[algorithms] Graph 圖

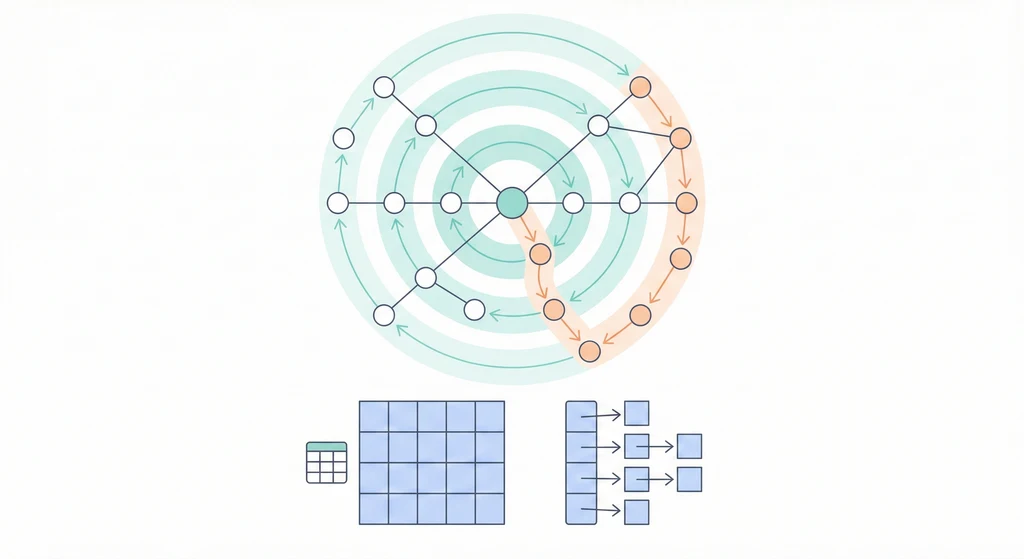
視覺化概覽

graph LR
    N1["1"] --- N2["2"]
    N1 --- N3["3"]
    N2 --- N4["4"]
    N3 --- N4
    N2 --- N5["5"]
    subgraph "BFS 從 1 開始"
        B["1 → 2,3 → 4,5"]
    end
    subgraph "DFS 從 1 開始"
        D["1 → 2 → 4 → 3 → 5"]
    end
    style N1 fill:#9f9,stroke:#333,stroke-width:2px
    style B fill:#bbf,stroke:#333
    style D fill:#f9f,stroke:#333

什麼是圖？

圖是由節點 (Vertex) 和邊 (Edge) 組成的結構，用來表示關係。

    1 --- 2
    |     |
    3 --- 4

節點：1, 2, 3, 4 邊：(1,2), (1,3), (2,4), (3,4)

圖的類型

類型	說明
無向圖	邊沒有方向，A-B = B-A
有向圖	邊有方向，A→B ≠ B→A
有權圖	邊有權重（距離、成本等）
無環圖	沒有環路

無向圖:         有向圖:
1 --- 2        1 → 2
|     |        ↓   ↓
3 --- 4        3 → 4

圖的表示方式

1. 鄰接矩陣 (Adjacency Matrix)

用 2D 陣列，matrix[i][j] = 1 表示 i 和 j 有邊。

    1  2  3  4
1 [ 0, 1, 1, 0 ]
2 [ 1, 0, 0, 1 ]
3 [ 1, 0, 0, 1 ]
4 [ 0, 1, 1, 0 ]

優點：查詢 O(1) 缺點：空間 O(V²)，稀疏圖浪費

2. 鄰接表 (Adjacency List)

每個節點存一個鄰居列表。

1 → [2, 3]
2 → [1, 4]
3 → [1, 4]
4 → [2, 3]

優點：空間 O(V + E) 缺點：查詢 O(V)

比較

操作	鄰接矩陣	鄰接表
空間	O(V²)	O(V + E)
查詢邊	O(1)	O(V)
遍歷鄰居	O(V)	O(degree)
適用	稠密圖	稀疏圖

圖的遍歷

BFS 廣度優先搜尋

像水波一樣，一圈一圈往外擴。 用 Queue。

從 1 開始:
    1          第1層: 1
   / \         第2層: 2, 3
  2   3        第3層: 4
   \ /
    4

BFS: [1, 2, 3, 4]

Queue<Integer> queue = new LinkedList<>();
queue.add(start);
visited.add(start);
 
while (!queue.isEmpty()) {
    int v = queue.poll();
    for (int neighbor : graph.get(v)) {
        if (!visited.contains(neighbor)) {
            visited.add(neighbor);
            queue.add(neighbor);
        }
    }
}

DFS 深度優先搜尋

一條路走到底，再回頭。 用 Stack 或遞迴。

從 1 開始:
    1     1 → 2 → 4 → 3 (走到底)
   / \    回頭發現 3 已走過
  2   3
   \ /
    4

DFS: [1, 2, 4, 3]

void dfs(int v) {
    visited.add(v);
    for (int neighbor : graph.get(v)) {
        if (!visited.contains(neighbor)) {
            dfs(neighbor);
        }
    }
}

BFS vs DFS

比較	BFS	DFS
資料結構	Queue	Stack/遞迴
特性	找最短路徑	找所有路徑
空間	O(V) 寬度	O(V) 深度
用途	最短路、層序	拓撲排序、環檢測

時間複雜度

操作	時間
BFS	O(V + E)
DFS	O(V + E)
新增邊	O(1)
查詢邊	O(V) 鄰接表 / O(1) 鄰接矩陣

經典應用

應用	演算法
最短路徑	BFS (無權), Dijkstra (有權)
拓撲排序	DFS
環檢測	DFS
連通分量	BFS/DFS
最小生成樹	Prim, Kruskal

相關檔案

• Java 實作：Graph.java
• 視覺化：graph.html