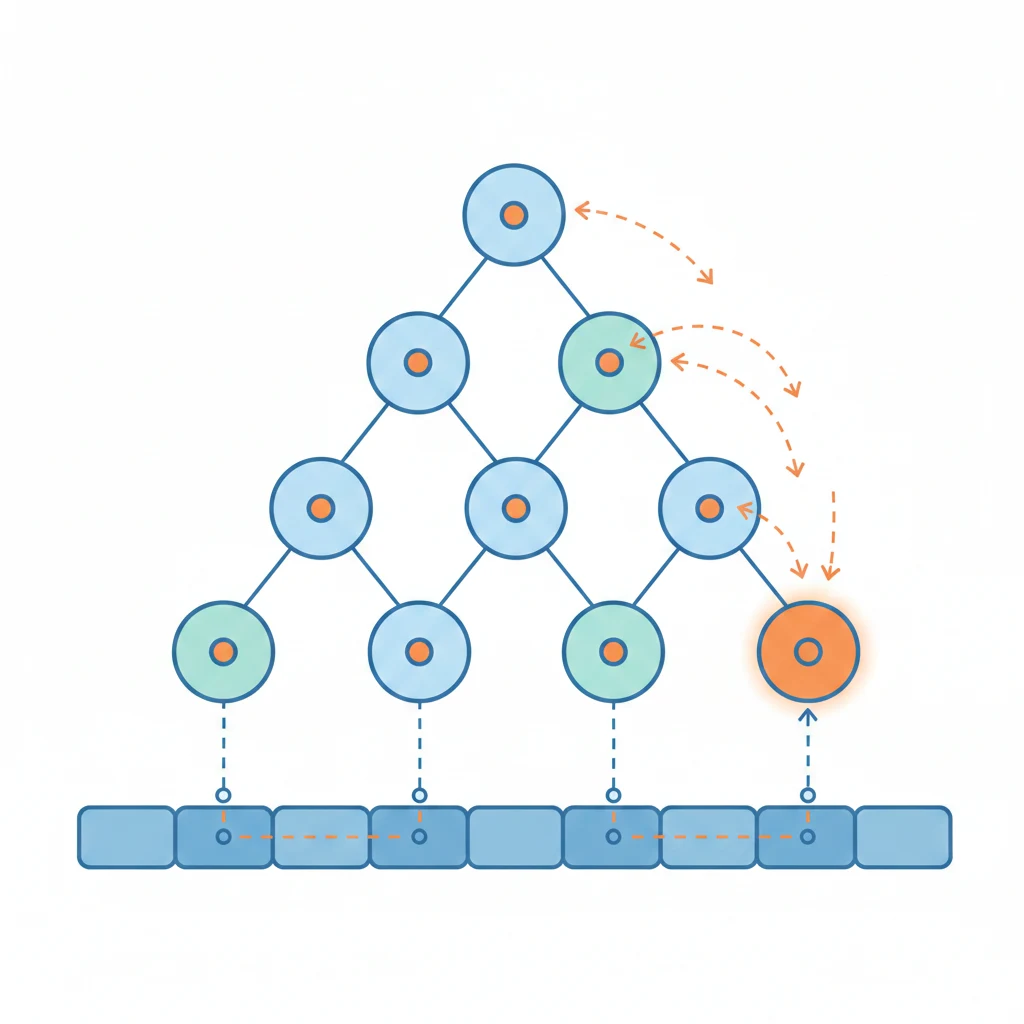
視覺化概覽
graph TD N10["10 (根=最小)"] --> N20["20"] N10 --> N30["30"] N20 --> N40["40"] N20 --> N50["50"] INS["插入 15"] -.->|"加到最後 → 上浮"| N50 EXT["取出 10"] -.->|"取根 → 末尾補上 → 下沉"| N10 style N10 fill:#9f9,stroke:#333,stroke-width:2px style INS fill:#bbf,stroke:#333 style EXT fill:#f99,stroke:#333
什麼是堆?
堆是一種完全二元樹,滿足堆性質:
- Min-Heap:父節點 ⇐ 子節點(根是最小值)
- Max-Heap:父節點 >= 子節點(根是最大值)
Min-Heap: Max-Heap:
10 90
/ \ / \
20 30 70 80
/ \ / \
40 50 50 60
為什麼用陣列實作?
完全二元樹可以用陣列緊湊表示,不需要指標!
樹的結構: 陣列表示:
10 [10, 20, 30, 40, 50]
/ \ 0 1 2 3 4
20 30
/ \
40 50
索引公式
| 關係 | 公式 |
|---|---|
| 父節點 | (i - 1) / 2 |
| 左子節點 | 2 * i + 1 |
| 右子節點 | 2 * i + 2 |
[0]
/ \
[1] [2]
/ \ / \
[3] [4] [5] [6]
index=4 的父節點: (4-1)/2 = 1
index=1 的左子節點: 2*1+1 = 3
index=1 的右子節點: 2*1+2 = 4
核心操作
| 操作 | 時間 | 說明 |
|---|---|---|
| insert | O(log n) | 加到最後,上浮 |
| extract | O(log n) | 取根,用最後一個替代,下沉 |
| peek | O(1) | 看根節點 |
| build | O(n) | 從陣列建堆 |
Insert 操作
插入 15 到 Min-Heap [10, 20, 30, 40, 50]:
Step 1: 加到最後
[10, 20, 30, 40, 50, 15]
↑ 新加入
Step 2: 上浮 (Bubble Up)
15 < 30? Yes → 交換
[10, 20, 15, 40, 50, 30]
↑
15 < 10? No → 停止
最終: [10, 20, 15, 40, 50, 30]
Extract 操作
從 Min-Heap [10, 20, 30, 40, 50] 取出最小值:
Step 1: 取出根節點 10
Step 2: 把最後一個 (50) 移到根
[50, 20, 30, 40]
↑
Step 3: 下沉 (Bubble Down)
50 > min(20, 30)? Yes → 和 20 交換
[20, 50, 30, 40]
↑
50 > 40? Yes → 交換
[20, 40, 30, 50]
最終: [20, 40, 30, 50]
回傳: 10
Heap vs BST
| 比較 | Heap | BST |
|---|---|---|
| 結構 | 完全二元樹 | 任意形狀 |
| 找最小/最大 | O(1) | O(log n) |
| 搜尋任意值 | O(n) | O(log n) |
| 插入 | O(log n) | O(log n) |
| 用途 | Priority Queue | 排序、搜尋 |
重點:Heap 只保證根是最小/最大,不保證整體有序。
經典應用
1. Priority Queue 優先佇列
PriorityQueue<Task> pq = new PriorityQueue<>();
pq.add(task); // O(log n)
Task urgent = pq.poll(); // O(log n) 取出最優先的2. Heap Sort
// 建立 Max-Heap,依序取出最大值
for (int i = n-1; i >= 0; i--) {
arr[i] = heap.extract(); // 放到已排序區
}
// 時間 O(n log n),空間 O(1)3. Top K 問題
找最大的 K 個元素:
// 用大小為 K 的 Min-Heap
// 只保留最大的 K 個4. 合併 K 個有序列表
// 用 Min-Heap 維護 K 個列表的當前最小值Build Heap 為什麼是 O(n)?
逐一插入是 O(n log n),但從陣列建堆只需 O(n)!
// 從最後一個非葉節點開始,往上 heapify
for (int i = n/2 - 1; i >= 0; i--) {
bubbleDown(i);
}原因:大部分節點在底層,只需少量操作。