[algorithms] Stack 堆疊

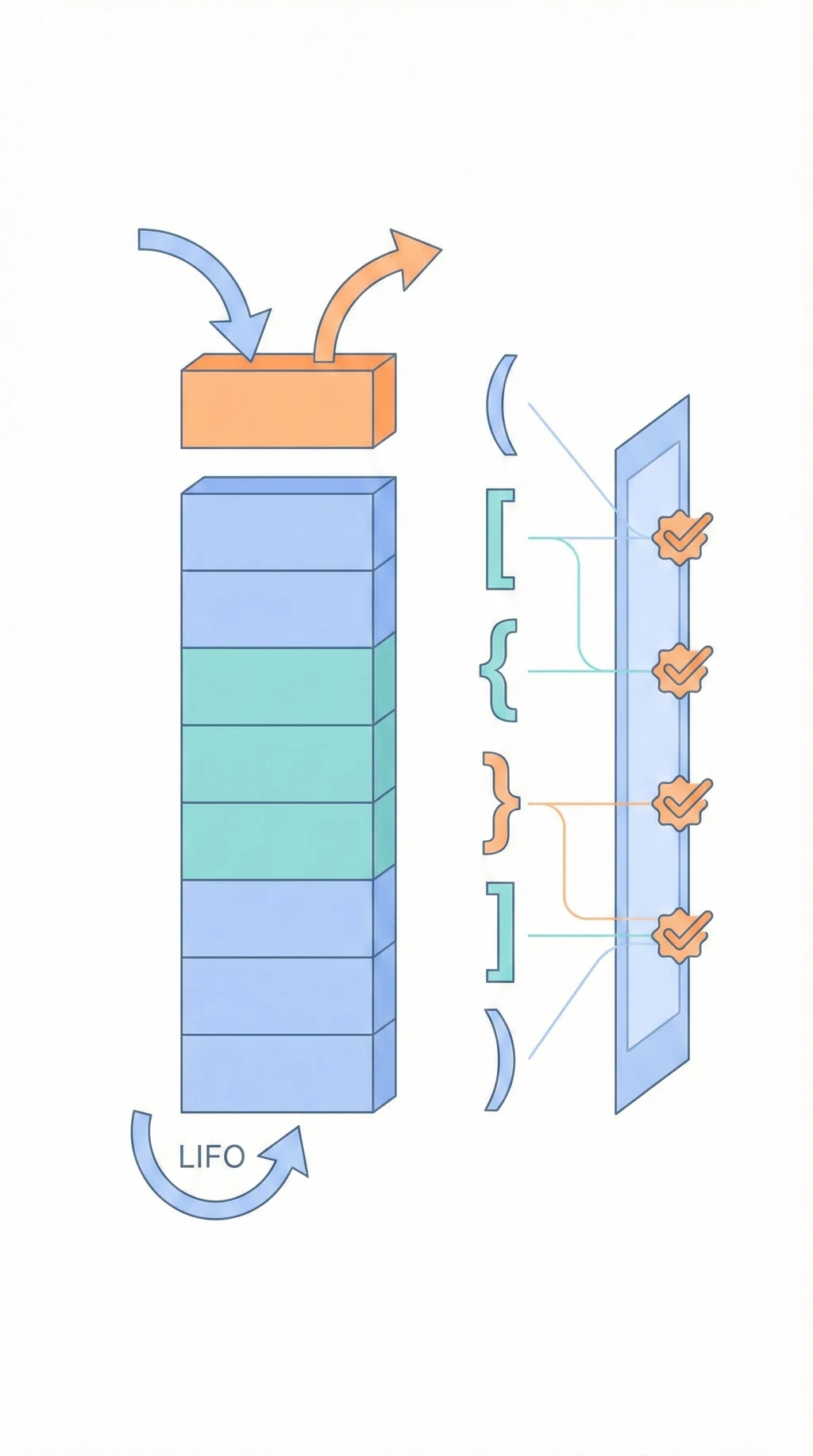
視覺化概覽

graph TD
    PUSH["push(40)"] -.-> TOP
    TOP["頂端 → 30"] --> MID["20"] --> BOT["10"]
    TOP2["頂端 → 40"] --> E30["30"] --> E20["20"] --> E10["10"]
    POP["pop() = 40"] -.-> TOP2
    subgraph 操作前
        TOP
        MID
        BOT
    end
    subgraph 操作後
        TOP2
        E30
        E20
        E10
    end
    style PUSH fill:#9f9,stroke:#333
    style POP fill:#f99,stroke:#333

💡 白話版：Stack 就像一疊盤子。最後放上去的最先拿走（LIFO）。你瀏覽器的「上一頁」就是用 Stack 做的。

什麼是堆疊？

堆疊就像一疊盤子，只能從最上面放、從最上面拿。

後進先出 (LIFO - Last In First Out)

      ┌────┐
      │ 30 │  ← top（最後放的，最先拿）
      ├────┤
      │ 20 │
      ├────┤
      │ 10 │  ← bottom（最先放的，最後拿）
      └────┘

核心操作

操作	說明	時間
push(x)	放入元素到頂端	O(1)
pop()	取出頂端元素	O(1)
peek()	查看頂端（不取出）	O(1)
isEmpty()	是否為空	O(1)

所有操作都是 O(1)！

Push 操作

push(40):

      ┌────┐
      │ 30 │  top            ┌────┐
      ├────┤          →      │ 40 │  ← 新的 top
      │ 20 │                 ├────┤
      ├────┤                 │ 30 │
      │ 10 │                 ├────┤
      └────┘                 │ 20 │
                             ├────┤
                             │ 10 │
                             └────┘

Pop 操作

pop() = 30:

      ┌────┐
      │ 30 │  ← 取出          ┌────┐
      ├────┤          →      │ 20 │  ← 新的 top
      │ 20 │                 ├────┤
      ├────┤                 │ 10 │
      │ 10 │                 └────┘
      └────┘

實作方式

用 Array 實作

class Stack {
    Object[] data;
    int top = 0;  // 指向下一個要放的位置
 
    void push(x) { data[top++] = x; }
    Object pop() { return data[--top]; }
}

用 Linked List 實作

class Stack {
    Node head;  // 頭就是 top
 
    void push(x) { addFirst(x); }
    Object pop() { return removeFirst(); }
}

經典應用

1. 括號匹配

輸入: {[()]}
過程:
  { → push('{')      stack: ['{']
  [ → push('[')      stack: ['{', '[']
  ( → push('(')      stack: ['{', '[', '(']
  ) → pop() = '('    stack: ['{', '[']     ✓ 匹配
  ] → pop() = '['    stack: ['{']          ✓ 匹配
  } → pop() = '{'    stack: []             ✓ 匹配
結果: stack 為空 → 匹配成功！

2. 瀏覽器上一頁/下一頁

瀏覽: A → B → C
back stack: [A, B, C]  ← 目前在 C

按「上一頁」:
  pop() = C → 存到 forward stack
  peek() = B → 顯示 B

3. 撤銷操作 (Undo)

每次操作 push 到 stack，Undo 就 pop。

4. 函數呼叫堆疊 (Call Stack)

void a() { b(); }
void b() { c(); }
void c() { ... }
 
Call Stack:
  c()  ← 目前執行
  b()
  a()
  main()

什麼時候用 Stack？

• 需要「最後處理的先完成」的場景
• 遞迴改迭代
• 深度優先搜尋 (DFS)
• 表達式求值

相關檔案

• Java 實作：Stack.java
• 視覺化：stack.html