[algorithms] Math Algorithms 數學演算法

視覺化概覽

flowchart TD
    A["歐幾里得算法\ngcd(48, 18)"] --> B["a=48, b=18\n48 % 18 = 12"]
    B --> C["a=18, b=12\n18 % 12 = 6"]
    C --> D["a=12, b=6\n12 % 6 = 0"]
    D --> E{"b == 0？"}
    E -- 是 --> F["回傳 a = 6\ngcd(48,18) = 6"]
    E -- 否 --> G["繼續: a=b, b=a%b"]
    G --> B

    style F fill:#90EE90

GCD / LCM

歐幾里得算法

int gcd(int a, int b) {
    while (b != 0) {
        int temp = b;
        b = a % b;
        a = temp;
    }
    return a;
}
 
long lcm(int a, int b) {
    return (long) a / gcd(a, b) * b;
}

gcd(48, 18):
48 % 18 = 12
18 % 12 = 6
12 % 6  = 0  → gcd = 6

質數

判斷質數 O(√n)

boolean isPrime(int n) {
    if (n < 2) return false;
    if (n < 4) return true;
    if (n % 2 == 0 || n % 3 == 0) return false;
    for (int i = 5; i * i <= n; i += 6) {
        if (n % i == 0 || n % (i + 2) == 0) return false;
    }
    return true;
}

埃拉托斯特尼篩法 O(n log log n)

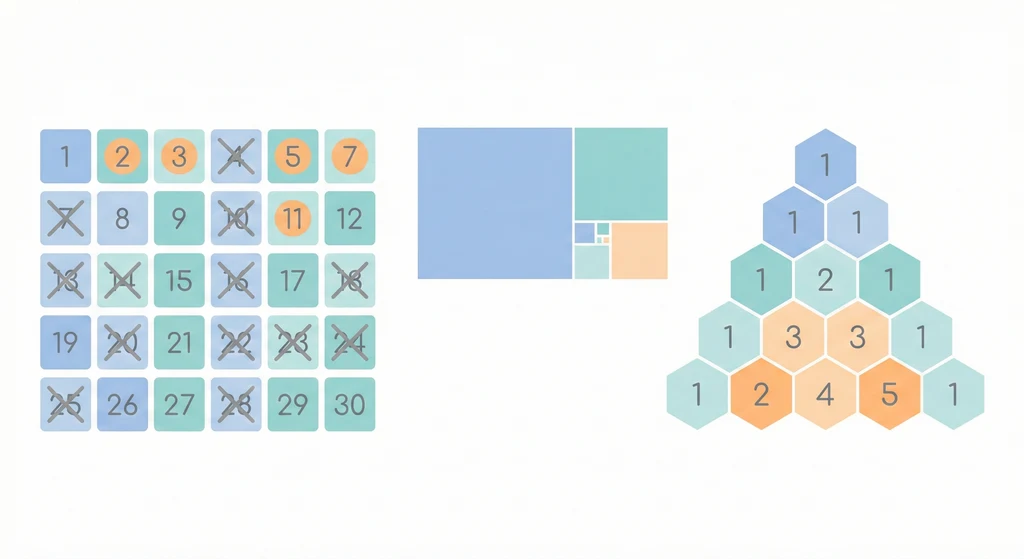
篩 30 以內的質數：
2  3  4  5  6  7  8  9  10 ...
2  3  ✗  5  ✗  7  ✗  ✗  ✗  ...  ← 篩掉 2 的倍數
2  3     5     7     ✗      ...  ← 篩掉 3 的倍數
2  3     5     7            ...  ← 篩掉 5 的倍數（從 25 開始）

結果: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29

快速冪

// O(log n) 計算 base^exp % mod
long modPow(long base, long exp, long mod) {
    long result = 1;
    base %= mod;
    while (exp > 0) {
        if ((exp & 1) == 1)
            result = result * base % mod;
        exp >>= 1;
        base = base * base % mod;
    }
    return result;
}

2^10 的計算過程：
10 = 1010₂
2^10 = 2^8 × 2^2 = 256 × 4 = 1024

exp=10(1010): result=1, base=2
exp=5 (101):  result=1×4=4, base=4
exp=2 (10):   result=4, base=16
exp=1 (1):    result=4×256=1024, base=65536

排列組合

組合數

// C(n, k) = n! / (k! × (n-k)!)
long combination(int n, int k) {
    k = Math.min(k, n - k);
    long result = 1;
    for (int i = 0; i < k; i++) {
        result = result * (n - i) / (i + 1);
    }
    return result;
}

帕斯卡三角

         1
        1 1
       1 2 1
      1 3 3 1
     1 4 6 4 1

C(n, k) = C(n-1, k-1) + C(n-1, k)

矩陣快速冪

加速線性遞推式，如 Fibonacci：

[F(n+1)]   [1 1]^n   [F(1)]
[F(n)  ] = [1 0]   × [F(0)]

O(log n) 求第 n 個 Fibonacci 數。

進位轉換

String toBase(int num, int base) {
    StringBuilder sb = new StringBuilder();
    while (num > 0) {
        int digit = num % base;
        sb.append(digit < 10 ? (char)('0' + digit) : (char)('A' + digit - 10));
        num /= base;
    }
    return sb.reverse().toString();
}

常用公式

公式	說明
1+2+…+n = n(n+1)/2	等差數列
a^1+…+a^n = a(a^n-1)/(a-1)	等比數列
C(n,k) = C(n-1,k-1)+C(n-1,k)	組合遞推
(a+b)%m = (a%m+b%m)%m	模運算性質
(a×b)%m = (a%m×b%m)%m	模運算性質

經典題目

1. Pow(x, n) - LeetCode 50
2. 計數質數 - LeetCode 204
3. 快樂數 - LeetCode 202
4. 楊輝三角 - LeetCode 118
5. 階乘後的零 - LeetCode 172
6. GCD / LCM - 基礎數論
7. 進制轉換 - 各種進制
8. 矩陣快速冪 - 加速遞推

相關檔案

• Java 實作：MathAlgorithms.java