[algorithms] Prefix Sum 前綴和 & Difference Array 差分陣列

視覺化概覽

flowchart TD
    A["原始陣列\n[1, 2, 3, 4, 5]"] --> B["建立前綴和\nprefix[i+1] = prefix[i] + nums[i]"]
    B --> C["前綴和陣列\n[0, 1, 3, 6, 10, 15]"]
    C --> D["區間查詢: sum[1..3] = ?"]
    D --> E["prefix[4] - prefix[1]\n= 10 - 1 = 9"]
    E --> F["答案: 2+3+4 = 9 ✓\nO(1) 查詢！"]

    style A fill:#FFD700
    style C fill:#87CEEB
    style F fill:#90EE90

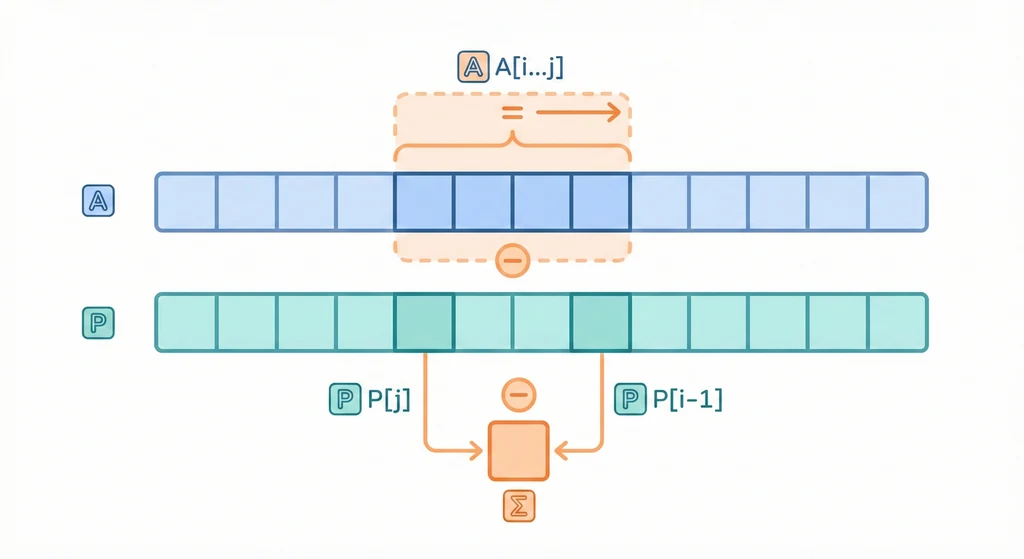
什麼是前綴和？

前綴和將「區間求和」問題從 O(n) 優化到 O(1)，只需 O(n) 預處理。

原始陣列:  [1, 2, 3, 4, 5]
前綴和:  [0, 1, 3, 6, 10, 15]
           ↑
         prefix[0] = 0（哨兵）

區間和 [1,3] = prefix[4] - prefix[1] = 10 - 1 = 9  (2+3+4)

一維前綴和

// 建立
long[] prefix = new long[n + 1];
for (int i = 0; i < n; i++) {
    prefix[i + 1] = prefix[i] + nums[i];
}
 
// 查詢 [left, right]
long sum = prefix[right + 1] - prefix[left];

二維前綴和

矩陣:            前綴和:
1  2  3          0  0  0  0
4  5  6          0  1  3  6
7  8  9          0  5  12 21
                 0  12 27 45

查詢 (r1,c1) 到 (r2,c2):
sum = prefix[r2+1][c2+1]
    - prefix[r1][c2+1]
    - prefix[r2+1][c1]
    + prefix[r1][c1]

    ┌──────────────────┐
    │  A  │     B       │ c2+1
    ├─────┼─────────────┤
    │  C  │  目標區域    │ r2+1
    └─────┴─────────────┘
          c1

    目標 = 全部 - B - C + A

差分陣列

差分陣列是前綴和的逆運算。用於 O(1) 區間更新。

原始:    [0, 0, 0, 0, 0]
差分:    [0, 0, 0, 0, 0]

操作: [1,3] += 2
差分:    [0, 2, 0, 0, -2]
還原:    [0, 2, 2, 2, 0]

操作: [2,4] += 3
差分:    [0, 2, 3, 0, -2]
還原:    [0, 2, 5, 5, 3]

// 區間加值
diff[left] += val;
if (right + 1 < n) diff[right + 1] -= val;
 
// 還原
for (int i = 1; i < n; i++) {
    result[i] = result[i-1] + diff[i];
}

前綴和 + HashMap

和為 K 的子陣列個數

int subarraySum(int[] nums, int k) {
    Map<Long, Integer> map = new HashMap<>();
    map.put(0L, 1);  // 前綴和為 0 出現 1 次
    long sum = 0;
    int count = 0;
 
    for (int num : nums) {
        sum += num;
        // 如果 sum - k 出現過，代表存在子陣列和為 k
        count += map.getOrDefault(sum - k, 0);
        map.merge(sum, 1, Integer::sum);
    }
    return count;
}

對比

	前綴和	差分陣列
預處理	O(n)	O(n)
單點查詢	O(1)	O(n) 需還原
區間查詢	O(1)	-
區間更新	O(n)	O(1)
適用場景	多次查詢	多次更新

經典題目

1. 區域和檢索 - LeetCode 303
2. 二維區域和 - LeetCode 304
3. 和為 K 的子陣列 - LeetCode 560
4. 能被 K 整除的子陣列 - LeetCode 974
5. 連續的子陣列和 - LeetCode 523
6. 航班預訂統計（差分） - LeetCode 1109
7. 拼車（差分） - LeetCode 1094

相關檔案

• Java 實作：PrefixSum.java