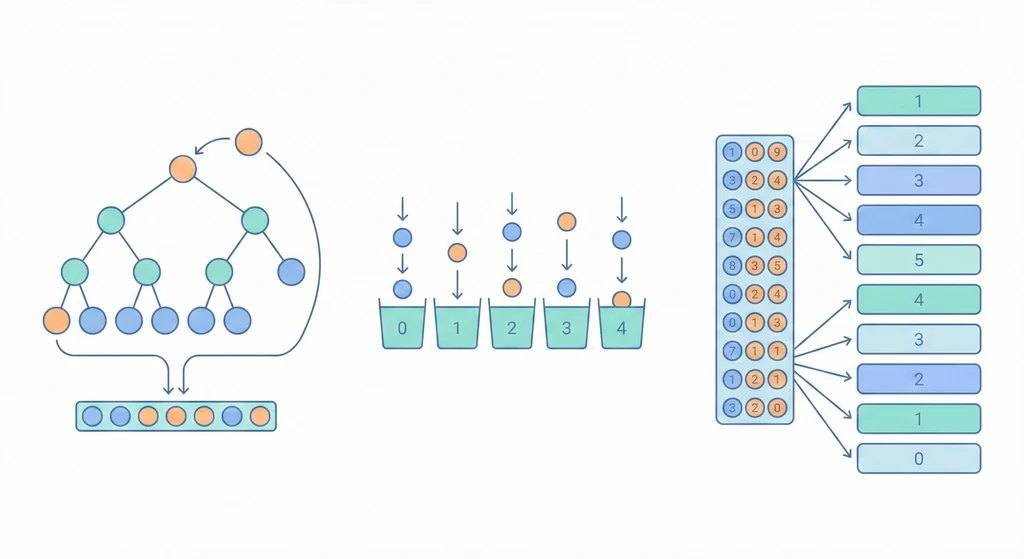
視覺化概覽
flowchart TD A["原始陣列: [4, 2, 2, 8, 3, 3, 1]"] --> B["步驟1: 計數\n統計每個值出現次數"] B --> C["count 陣列\n[0,1,2,2,1,0,0,0,1]\n idx: 0 1 2 3 4 5 6 7 8"] C --> D["步驟2: 累加\n計算每個值的最終位置"] D --> E["累加陣列\n[0,1,3,5,6,6,6,6,7]"] E --> F["步驟3: 輸出\n反向遍歷原陣列,放入正確位置"] F --> G["排序結果: [1, 2, 2, 3, 3, 4, 8]"]
排序演算法分類
比較排序 O(n log n) 下界
- Heap Sort、Merge Sort、Quick Sort、Shell Sort
非比較排序 O(n)(特定條件)
- Counting Sort、Radix Sort、Bucket Sort
1. Heap Sort 堆積排序
利用堆的性質排序
建立最大堆 → 取出最大值 → 調整堆 → 重複
[4, 10, 3, 5, 1]
10
/ \
5 3
/ \
4 1
取出 10,調整...
void heapSort(int[] arr) {
// 建堆
for (int i = n/2-1; i >= 0; i--)
heapify(arr, n, i);
// 取出排序
for (int i = n-1; i > 0; i--) {
swap(arr, 0, i);
heapify(arr, i, 0);
}
}特點:O(n log n),原地,不穩定
2. Counting Sort 計數排序
統計每個值出現次數
[4, 2, 2, 8, 3, 3, 1]
count: [0, 1, 2, 2, 1, 0, 0, 0, 1]
0 1 2 3 4 5 6 7 8
結果: [1, 2, 2, 3, 3, 4, 8]
// 計數
for (int num : arr) count[num]++;
// 累加(穩定排序用)
for (int i = 1; i < k; i++) count[i] += count[i-1];
// 輸出
for (int i = n-1; i >= 0; i--) {
output[count[arr[i]] - 1] = arr[i];
count[arr[i]]--;
}特點:O(n + k),k = 值域,穩定
適用:整數,值域不大
3. Radix Sort 基數排序
按位數排序,低位到高位
[170, 45, 75, 90, 802, 24, 2, 66]
按個位: [170, 90, 802, 2, 24, 45, 75, 66]
按十位: [802, 2, 24, 45, 66, 170, 75, 90]
按百位: [2, 24, 45, 66, 75, 90, 170, 802]
for (int exp = 1; max/exp > 0; exp *= 10) {
countingSortByDigit(arr, exp);
}特點:O(d × (n + k)),d = 位數,穩定
適用:整數,位數固定
4. Bucket Sort 桶排序
分桶 → 桶內排序 → 合併
[0.42, 0.32, 0.23, 0.52, 0.25]
桶 0: []
桶 1: []
桶 2: [0.23, 0.25]
桶 3: [0.32]
桶 4: [0.42]
桶 5: [0.52]
...
特點:O(n + k) 平均,最差 O(n²)
適用:均勻分佈的數據
5. Shell Sort 希爾排序
帶間隔的插入排序
[12, 34, 54, 2, 3]
gap=2: 比較 12-54, 34-2, 54-3
[12, 2, 3, 34, 54]
gap=1: 普通插入排序
[2, 3, 12, 34, 54]
特點:O(n^1.3),原地,不穩定
6. Tim Sort
Python 和 Java 預設使用。
混合排序:插入 + 歸併
- 分成小段(run)
- 小段用插入排序
- 用歸併合併
特點:O(n) 最佳(近乎有序),O(n log n) 平均
複雜度對比
| 演算法 | 時間 | 空間 | 穩定 |
|---|---|---|---|
| Heap Sort | O(n log n) | O(1) | 否 |
| Counting Sort | O(n + k) | O(k) | 是 |
| Radix Sort | O(d(n+k)) | O(n+k) | 是 |
| Bucket Sort | O(n + k) | O(n) | 是 |
| Shell Sort | O(n^1.3) | O(1) | 否 |
| Tim Sort | O(n log n) | O(n) | 是 |
選擇指南
數據類型?
├─ 整數
│ ├─ 值域小 → Counting Sort
│ └─ 位數固定 → Radix Sort
├─ 浮點數,均勻分佈 → Bucket Sort
└─ 通用
├─ 空間限制 → Heap Sort
├─ 需要穩定 → Merge Sort
├─ 幾乎有序 → Tim Sort / Insertion Sort
└─ 一般情況 → Quick Sort
相關檔案
- Java 實作:MoreSorting.java
- 基礎排序:Sorting.java